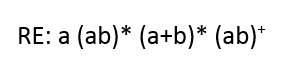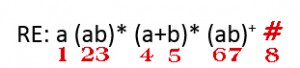RE – DFA
Soal:
Buat RE -> DFA dengan 2 cara:
- Menggunakan cara tree
- Cara ε – NFA
Setelah itu lakukan DFA minimized.
Constraint:
- State dari DFA minimal 5 state maksimal 8 state.
- Final state minimal 2 state dan maksimal 3 state
Jawaban:
1. Menggunakan cara tree
Tentukan index terlebih dahulu:
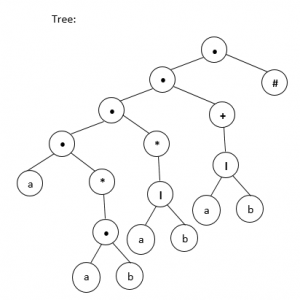
Buat tree-nya:
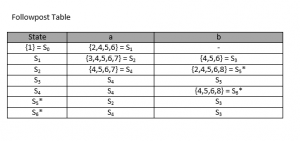
Kemudian, tentukan followpost masing – masing index:
- Follow post 1 = 2, 4, 5, 6
- Follow post 2 = 3
- Follow post 3 = 2, 4, 5, 6
- Follow post 4 = 4, 5, 6
- Follow post 5 = 4, 5, 6
- Follow post 6 = 7
- Follow post 7 = 6, 8
- Follow post 8 = –
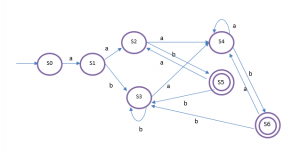
Berdasarkan followpost di atas, tentukan state – statenya:
Hasil DFA:
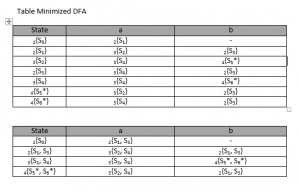
DFA di atas masih dapat kita minimalisasi dengan melakukan grouping, sebagai berikut:
Hasil DFA setelah diminimized:
2. Menggunakan cara ε – NFA
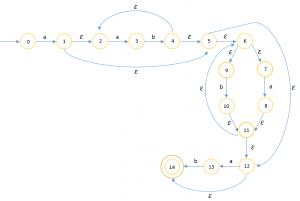
Pertama, buat ε – NFAnya:
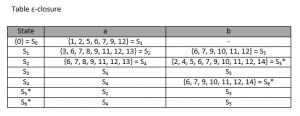
Kemudian cari ε-closure movenya:
- ε-closure (0) = 0 → {S0}
- ε-closure (move(S0, a)) = ε-closure {1} = {1, 2, 5, 6, 7, 9, 12} → {S1}
- ε-closure (move(S0, b)) = {}
- ε-closure (move(S1, a)) = ε-closure {3, 8, 13} = {3, 6, 7, 8, 9, 11, 12, 13} → {S2}
- ε-closure (move(S1, b)) = ε-closure {10} = {6, 7, 9, 10, 11, 12} → {S3}
- ε-closure (move(S2, a)) = ε-closure {8, 13} = {6, 7, 8, 9, 11, 12, 13} → {S4}
- ε-closure (move(S2, b)) = ε-closure {4, 10, 14} = {2, 4, 5, 6, 7, 9, 10, 11, 12, 14} → {S5*}
- ε-closure (move(S3, a)) = ε-closure {8, 13} = {S4}
- ε-closure (move(S3, b)) = ε-closure {10} ={S3}
- ε-closure (move(S4, a)) = ε-closure {8, 13} = {S4}
- ε-closure (move(S4, b)) = ε-closure {10, 14} = {6, 7, 9, 10, 11, 12, 14} → {S6*}
- ε-closure (move(S5, a)) = ε-closure {3, 8, 13} = {S2}
- ε-closure (move(S5, b)) = ε-closure {10} = {S3}
- ε-closure (move(S6, a)) = ε-closure {8, 13} = {S4}
- ε-closure (move(S6, b)) = ε-closure {10} = {S3}
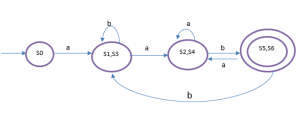
Dari langkah di atas dapat ditentukan jalur masing – masing statenya:
Hasil DFA: