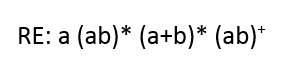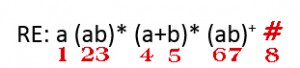Archive for the ‘Teknik Kompilasi’ Category
Code Generator
Assembly Code
01. mov a2,R0
02. mov a1,R1
03. mov b2,R2
04. mov b1,R3
05. sub R1,R0
06. mul R0,R0
07. sub R3,R2
08. mul R2,R2
09. add R2,R0
10. fsqrt R0
11. mov radius,R1
12. lt R0,R1
13. jmpf R1,(15)
14. prt (“Titik berada di luar lingkaran”)
15. gt R0,R1
16. jmpf R1,(19)
17. prt (“Titik berada di dalam lingkaran”)
18. jmp R1,(20)
19. prt (“Titik berada tepat pada lingkaran”)
20. ….
Tugas 3 – Teknik Kompilasi
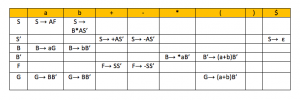
B → aB | B(a+B) | B*a |a(a+B)|b
S → A+SS’ | A – SS’ | B * AS’
S’ → +AS’ | -AS’ | ε
S → AF | B * AS’
F → +SS’ | -SS’
S’ → +AS’ | -AS’ | ε
B → aBB’ | a(a+B)B’ | bB’
B’→ (a+B)B’ | *aB’
B → aG | bB’
G → BB’ | (a+B)B’
B’ → (a+B)B’ | *aB’
A → a
First S → {a,b}
First F → {+,-}
First S’ → {+,-, ε}
First B → {a,b}
First G → {a,b,(}
First B’ → {(,*}
Follow S → {$,+,-}
Follow S’ → {$}
Follow B → {$,a,b,)}
Follow B’ → {$}
Follow F → {$,+,-}
Follow G → {$,a,b,)}
Table :
2.
S → if E then S | if E then sS else S | V:= E
V → id |id[E]
E → E+T |E-T|T
T → T*F|T/F|F
F → V|(E) |const
Tentukan First, Follow, dan tabel dari production diatas!
Jawaban:
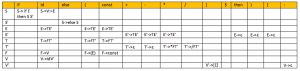
S → If E then SS’ | V:=E
S’ → ԑ | else S
V → idV’
V’→ ԑ|(E)
E → TE’
E’ → +TE’|-TE’| ԑ
T → FT’
T’→ *FT’ | /FT | ԑ
F → V|(E)| const
First (S) = {if, id}
First (S’) = {ε, else}
First (E) = { id, ( , const}
First (E’) = {+, -, ε}
First (T) = {id,(, const}
First (T’) = {*, /,ε }
First (F) = {id,(, const}
First (V) = {id}
First (V’) = {a b c}
Follow (S) = {$}
Follow (S’) = {$}
Follow (E) = { then, $,),]}
Follow (E’) = { then, $,),]}
Follow (T) = {+, -}
Follow (T’) = {+, -}
Follow (F) = {*,/ }
Follow (V) = {:}
Follow (V’) = {:}
Table:
3.S → a=A
A → aA’ |bA’
A’ → +AA’ | ԑ
Tentukan First, Follow, dan tabel dari production diatas!
Jawaban:
First (S) ={a}
First (A) = {a,b}
First (A’) = {+, ԑ}
Follow(S) ={$}
Follow(A) ={$, +}
Follow(A’) = {$, +}
Table:
4.
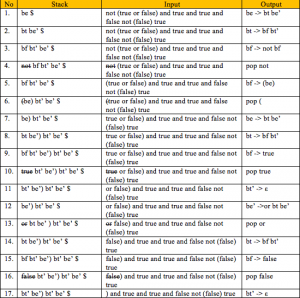
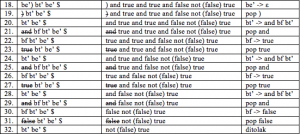
be → bt be’
be’ → or bt be’
be’ → ԑ
bt → bf bt’
bt’ → and bf bt’
bt’ → ԑ
bf → not bf
bf → (be)
bf → true
bf → false
Input : not(true or false) and true and true and false not (false) true
Jawaban:
First (be) = {not , ( , true , false}
First (be’) = {or , ε}
First (bt) = {not , ( , true , false}
First (bt’) = {and , ε}
First (bf) = {not , ( , true , false}
Follow (be) = {$ , )}
Follow (be’) = {$ , )}
Follow (bt) = {or , $ , )}
Follow (bt’) = {or , $ , )}
Follow (bf) = {or, $, ) , and}
Top-Down Parsing
Top-down parsing merupakan sebuah strategi untuk menganalisis data dari hipotesa umum struktur parse tree dan kemudian mempertimbangkan apakah struktur-struktur fundamental yang dikenal kompatibel dengan hipotesis. Contoh jenis parser yang menggunakan strategi parsing top-down adalah parser LL.
Mengapa Top – Down Parsing harus menghilangkan left-recursion & left-factoring?
Karena jika terdapat left-recursion dan left-factoring, akan terjadi ambiguitas pada saat top-down parser mencoba untuk mengurai input yang ambigu terhadap sebuah CFG dan juga memuungkinkan terjadinya looping terus menerus. Hal itu mungkin memerlukan beberapa langkah eksponensial untuk mencoba semua alternatif dari CFG untuk menghasilkan semua kemungkinan parse tree,, yang pada akhirnya akan membutuhkan ruang memori eksponensial (kompleksitas ruang bertambah). Dengan adanya ambiguitas, maka waktu pemrosesan menjadi lebih lama sehingga akan memunculkan masalah kompleksitas waktu.
RE – DFA
Soal:
Buat RE -> DFA dengan 2 cara:
- Menggunakan cara tree
- Cara ε – NFA
Setelah itu lakukan DFA minimized.
Constraint:
- State dari DFA minimal 5 state maksimal 8 state.
- Final state minimal 2 state dan maksimal 3 state
Jawaban:
1. Menggunakan cara tree
Tentukan index terlebih dahulu:
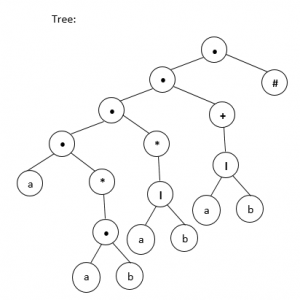
Buat tree-nya:
Kemudian, tentukan followpost masing – masing index:
- Follow post 1 = 2, 4, 5, 6
- Follow post 2 = 3
- Follow post 3 = 2, 4, 5, 6
- Follow post 4 = 4, 5, 6
- Follow post 5 = 4, 5, 6
- Follow post 6 = 7
- Follow post 7 = 6, 8
- Follow post 8 = –
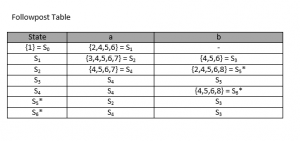
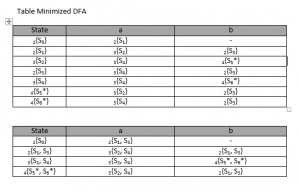
Berdasarkan followpost di atas, tentukan state – statenya:
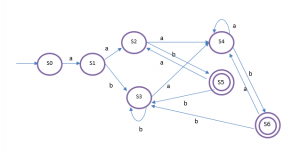
Hasil DFA:
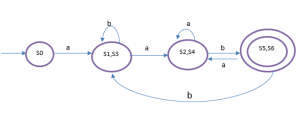
DFA di atas masih dapat kita minimalisasi dengan melakukan grouping, sebagai berikut:
Hasil DFA setelah diminimized:
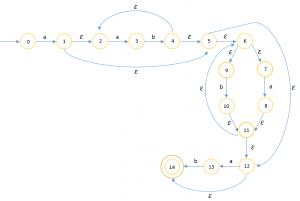
2. Menggunakan cara ε – NFA
Pertama, buat ε – NFAnya:
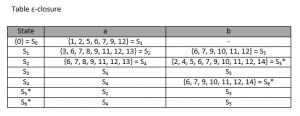
Kemudian cari ε-closure movenya:
- ε-closure (0) = 0 → {S0}
- ε-closure (move(S0, a)) = ε-closure {1} = {1, 2, 5, 6, 7, 9, 12} → {S1}
- ε-closure (move(S0, b)) = {}
- ε-closure (move(S1, a)) = ε-closure {3, 8, 13} = {3, 6, 7, 8, 9, 11, 12, 13} → {S2}
- ε-closure (move(S1, b)) = ε-closure {10} = {6, 7, 9, 10, 11, 12} → {S3}
- ε-closure (move(S2, a)) = ε-closure {8, 13} = {6, 7, 8, 9, 11, 12, 13} → {S4}
- ε-closure (move(S2, b)) = ε-closure {4, 10, 14} = {2, 4, 5, 6, 7, 9, 10, 11, 12, 14} → {S5*}
- ε-closure (move(S3, a)) = ε-closure {8, 13} = {S4}
- ε-closure (move(S3, b)) = ε-closure {10} ={S3}
- ε-closure (move(S4, a)) = ε-closure {8, 13} = {S4}
- ε-closure (move(S4, b)) = ε-closure {10, 14} = {6, 7, 9, 10, 11, 12, 14} → {S6*}
- ε-closure (move(S5, a)) = ε-closure {3, 8, 13} = {S2}
- ε-closure (move(S5, b)) = ε-closure {10} = {S3}
- ε-closure (move(S6, a)) = ε-closure {8, 13} = {S4}
- ε-closure (move(S6, b)) = ε-closure {10} = {S3}
Dari langkah di atas dapat ditentukan jalur masing – masing statenya:
Hasil DFA: